ソフトウエアテストの技法という本から一部抜粋して説明します。
目次
- ■ソフトウエアテストの原則
- ■心理学
- ■経済学
- ■ホワイトボックステスト
- ■ソフトウェアテストの原則
- ■プログラムの検査、ウォークスルー、検討
- ■検査とウォークスルー
- ■コードの検査
- ■検査のためのエラーチェックリスト
- ■ウォークスルー
- ■机上のチェック
- ■仲間内の評価
- ■テストケースの設計
- ■ブラックボックス
- ■ホワイトボックス
- ■推奨する手続き
- ■論理網羅テスト
- ■同値分割
- ■同値クラスの見極め方
- ■限界値分析
- ■原因結果グラフ
- ■エラー推測
- ■戦略
- ■モジュールのテスト
- ■テストケースの設計方法:増加テスト
- ■テストの実行
- ■上級テスト
- ■デバッグ
- ■エラーの位置発見の原則
- ■エラー修正の原則
- ■エラー分析
- ■補足
- ■参考
- ■経験則
- ■参考2
- ■プログラム
■ソフトウエアテストの原則
ソフトウエアテストはプログラマー自身が自分でテストをすることができないというのが常識です。
なぜならば自分は常に正しい、というふうに考えるからです。
■心理学
プログラムテストの心理学について説明します。
理想的にはプログラムの全てのロジックの組み合わせをテストしたいと考えますがそれは不可能です。
テストの心理学で重要なポイントはプログラムテストの定義を誤って理解している点です。
テストとはエラーがないことを示している過程であるとか、テストの目的はプログラムが意図された機能どおりに正しく動いてくれることを示すことであるとか、テストはプログラムが思いどおりに動く事の確信を作っていく過程であると考えています。
実際のところこれはテストについての正反対の定義です。
プログラムテストするということはテストによって付加価値をつけるということですから付加価値とは品質信頼性を向上させることです。
それはエラーを見つけそれを取り除くことです。
したがってテストはプログラムが作動することを示すためのものではなく、むしろプログラムエラーを含んでいるという仮定の下でテストを始めるべきです。
このように、テストを行う際には常に「エラーを見つける」姿勢を持つことが重要です。単なる確認作業ではなく、意図的に失敗や不具合を探し出すための活動であると認識しましょう。また、テストによって得られた知見は今後の開発工程や品質向上にも大きく寄与します。
したがってできるだけ多くのエラーを見つけるためにプログラムをテストするのです。
正しい定義はテストとはエラーを見つけるつもりでプログラムを実行する過程であると言えます。テストデータとしてはエラーを見つける確率の高いものを選ぶことです。
テストは破壊的な過程でありこれは我々の気性にも反していることになります。
大抵の人は作ることに心が向いていて破壊することはあまりやりたくないという気持ちが働いています。
またテストについての適切な定義をさらに補足するものとして、成功したとか、成功しないという言葉の使いかたを分析することです。ほとんどのプロジェクト管理者はエラーが見つからなかったテストケースを成功したテストと呼び、新しいエラーを見つけたテストを失敗と呼びます。
これは逆です。
テストはプログラムが思い通りに動くことを示して行く過程であるという常識的な定義のもつ問題は思い通りに動くプログラムであってもまだエラーを含みうる点であるということです。
もしプログラムが意図された動きをしない場合にはエラーが存在することは明白であるがプログラムが意図されなかった動きをする場合にもエラーが存在するのです。
まとめるとプログラムテストはプログラムの中のエラーを見つけようとする破壊的な過程であるということです。
■経済学
テストの経済学とは、全てのエラーを見つけるためのプログラムテストは可能か否かを決定することです。
どんな単純なプログラムであってもこれはノーです。
一般にプログラムすべてのエラーを見つけることは非現実的でありしばしば不可能でもあります。したがってテストする人がそのプログラムに対してもつ仮定と、テストケースを設計する方法をどうするかということです。
はじめに、戦略を立てることです。
一般的な戦略の二つはブラックボックステストとホワイトボックステストです。
ブラックボックステストはデータ依存テストとか入出力依存テストと呼ばれています。
これはプログラムをブラックボックスとみなして目標はプログラムの内部の構造と動作に一切関知しないでプログラムは仕様書通りの動きをしない状況を見つけることに関心を持つのです。
この方法ではテストデータは仕様書からだけ得られるということです。
このやり方でプログラムエラーを見つけようとすれば、徹底的な入力テストが基準になります。
例えばC++のコンパイラのブラックボックステストをやるとしましょう。
すべての正しいC++プログラムのテストケースを作らなければならないだけでなく事実上無限の数になりますが、すべての誤ったC++プログラムのテストケースを作ってこのコンパイラがそれを誤ったプログラムであることを確実に示すことができなければなりません。すなわちコンパイラが意図しない動き、例えば文法上誤りのあるプログラムを正確にコンパイルしないことを確実するテストをしなければなりません。メモリーを持つプログラム、例えばオペレーティングシステムやデータベースを用いたシステムなどにはもっと困った問題があります。
トランザクションの処理がその前の出来事に依存しているからです。
したがって全ての新しいトランザクションと正しくないトランザクションを試みなければならないばかりでなく、すべての可能なトランザクションの順序もテストしなければならないからです。
したがって徹底的入力テストは不可能であることがわかります。
1. プログラムは全くエラーを持たないと保証するようなテストができない。
2. プログラムテストの基本的な考え方には経済学的な見方が必要である。有限の数のテストで発見されるエラーを最大にすることによってテストに対する資源の成果を最大にすることを目的とすべきである。
■ホワイトボックステスト
ホワイトボックステストこれは論理依存テストと呼ばれていてプログラムの内部構造を調べるということです。プログラムの論理を調べることによりテストデータを作るということです。
プログラムすべての命令文が少なくとも1回実行されるようにすることを解答のように思われるだろうがこれは全く不適切です。
よく考えられるのは徹底的経路テストということです。
テストケースによってプログラムのすべての可能な制御経路を実行すればそのプログラムは完全にテストされたといってよいことになるのです。
しかしこの言い方には二つの欠点があります。
一つは、あるプログラムで異なった論理経路の数は天文学的な値である点です。
以前にも紹介しました簡単なプログラムを考えてみましょう。
このプログラムのブラックボックスのテストケースを考えてみます。
仕様は、
整数の個数を20までの数字として指定し、その数の整数を入力したのち最大値を出す。
という簡単なものです。
プログラムの中身を見ないでテストケースを作るとしたらどんなものですか?
皆さんは、正しいと思われるテストケースを入れて、正常であればテストは終了としませんか?
例えば、数字を5個入れてみて、テストする。
How many items? (1..20): 5
Number of integer: 5 (スペース区切り可):
1 2 55 3 4
Max is : 55
しかし、これだけではテストになりません。
のちに説明します限界値分析を使ってテストケースを作ると、
例
整数の数を指定する。N個
(1)0個
(2)1個の整数
(3)20個の整数
(4)19個の整数
(5)21個の整数
を指定。
入力する整数の数を、上記の指定した数を正確に入れてみる。
結果:
(1)
How many items? (1..20): 0
n is less than 1
(2)How many items? (1..20): 1
Number of integer: 1 (スペース区切り可):
5
Max is : 5
(3)
How many items? (1..20): 20
Number of integer: 20 (スペース区切り可):
1 2 3 4 55 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
Max is : 55
(4)
How many items? (1..20): 19
Number of integer: 19 (スペース区切り可):
How many items? (1..20): 19
Number of integer: 19 (スペース区切り可):
1 2 3 4 55 6 7 8 9 10 11 12 13 14 15 16 17 18 19
Max is : 55
(5)
How many items? (1..20): 21
n is too large’
このテストケースは失敗に終わっています。
なぜなら、整数の組み合わせに変化をもたしていないからです。
もし、このプログラムのループを固定の5にしていたらどうでしょうか?
今度は、プログラムの中を見てみましょう。
これはホワイトボックステストになります。
以下は、上記のプログラムのPASCALコードです。
program max_val;
uses SysUtils;
var
a: array[1..20] of Integer;
n, i, m: Integer;
begin
Write('How many items? (1..20): ');
ReadLn(n);
if (n > 20) then
begin
WriteLn('n is too large‘);
Exit;
end;
if (n < 1) then
begin
WriteLn(' n is less than 1');
Exit;
end;
WriteLn('Number of integer: ', n, ' (スペース区切り可):');
for i := 1 to n do
Read(a[i]);
m := a[1];
for i := 2 to n do
begin
if a[i] > m then
m := a[i];
end;
WriteLn('Max is : ', m);
end.
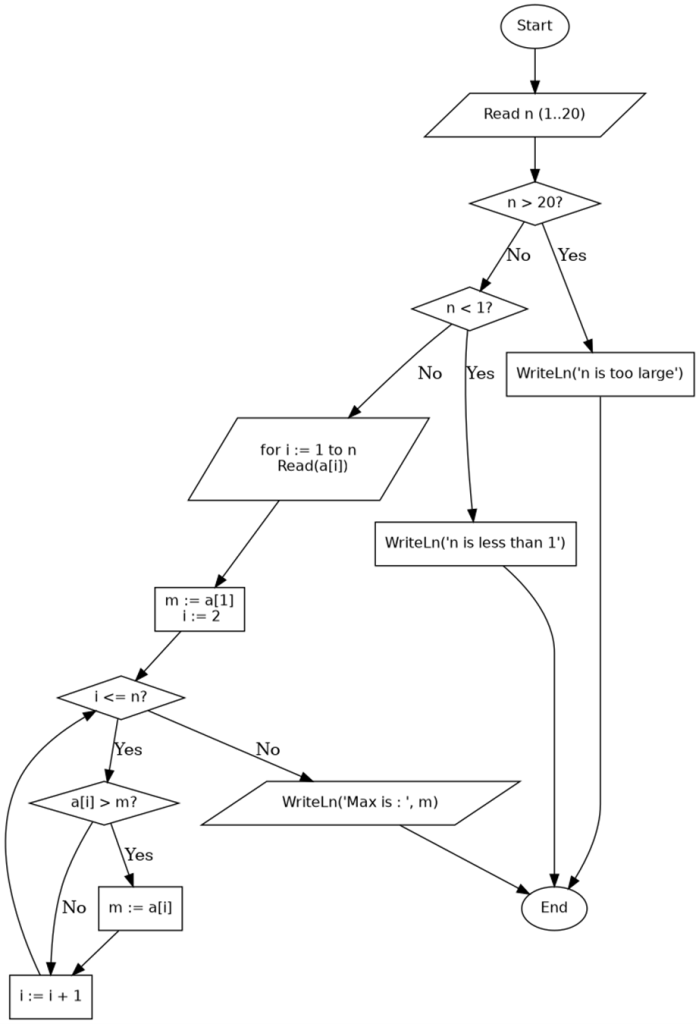
このフローチャートより、論理経路の数を計算してみます。
前提(カウントの基準)
• 「異なった論理経路」は if の分岐(Yes/No)の選択列で区別します。
• ループは n に依存して最大で n−1 回の反復を行い、各反復で if (a[i] > m?) が 2 通りに分岐します。
• n の検査(n > 20,n < 1)はそれぞれ別個の出口経路として数えます。
• 入力値の具体的な数値の等値性(複数の if が同じ結論を導く等)は考慮せず、分岐の取り方そのものを区別します。
1. 固定の n に対する経路数
• 正常ルート(1 ≤ n ≤ 20)のとき、ループの反復回数は n−1。各反復で if が 2 通りに分かれるので、 経路数 = 2^(n−1).
• 例: n=1 → 2^0 = 1 通り(ループは回らない)、n=2 → 2^1 = 2 通り、n=5 → 2^4 = 16 通り。
2. n の範囲全体(プログラム全体)での経路数
• n > 20 の場合は「n is too large」へ即終了:これは 1 通り
• n < 1 の場合は「n is less than 1」へ即終了:これも 1 通り
• 正常範囲は n = 1..20。それらを合計すると 合計正常経路 = sum_{n=1..20} 2^(n−1) = 2^20 − 1
• 全体合計 = (2^20 − 1) + 1 (too large) + 1 (too small) = 2^20 + 1
数値にすると
• 2^20 = 1,048,576
• よって 総経路数 = 1,048,576 + 1 = 1,048,577
まとめ
• 単一の n に対する経路数 = 2^(n−1)(1 ≤ n ≤ 20)
• プログラム全体(n を任意に取る、ただし分岐ルール通り集約)における異なる経路の総数 = 1,048,577
そこで徹底的入力テストと同様に徹底的経路テストは不可能とまで言わなくても非現実的であると思われます。
「徹底的経路テストが完全なテスト」を意味するという言い方の第2の欠点はプログラムの全ての経路が仮にテストできたとしても、そのプログラムはまだエラーを持っているということです。
第一は、徹底的経路テストでは決してプログラムが仕様と一致することを保証できないということです。一例として昇順に相当するサブルーチンを作成するように頼まれたが、うっかり降順にするサブプログラムを作ってしまったこと。
徹底的経路テストはほとんど無価値となる場合があります。
このプログラムは一つのバグつまり仕様と合わないということから、これは誤ったプログラムというバグを持っています。
第二は、経路を抜かすことによるプログラムの誤りがある。もちろんこの場合、徹底的経路テストは必要な経路が抜けていることを検出することはできないでしょう。
第三は、徹底的経路テストでもデータに依存するエラーは発見できない事である。
結論として、徹底的入力テストは徹底的経路テストにも勝るものではあるけれどもどちらも実行不可能であるという点で役に立つ方法とは言い難い。
参考2に本にあるフローチャートのグラフから論理経路の計算のためのプログラムとその結果を載せておきます。
■ソフトウェアテストの原則
原則1
テストケースの必須条件は予想される出力または結果を定義しておくことである。
原則2
プログラマーは自分自身のプログラムをテストしてはならない。
原則3
プログラム開発グループは自分たちのプログラムをテストしてはいけない。
原則4
それぞれのテスト結果を完全に検査せよ、
原則5
テストケースは予想できる正しい入力条件ばかりでなく予想しない誤った場合も考えて書かなければならない。
原則6
プログラムを調べるのにそれが意図されたように動くかを見ただけでは半ば成功したに過ぎない。残りの半分は意図されなかった動きをするかどうかを調べることである。
原則7
プログラムが本当に使い捨てのものでない限りそのテストケースも使い捨てにしてはならない。
原則8
エラーは見つからないだろうという仮定のもとにテストの計画を立ててはいけない。
原則9
プログラムのある部分でエラーがまだ存在している確率は既にその部分で見つかったエラーの数に比例する。
原則10
テストとは非常に創造的であり知的に挑戦しがいのある仕事である。
大きなプログラムをテストするのに必要とされる想像力はそのプログラムを設計するときに必要な想像力を凌ぐということは多分事実であろう。
プログラムのために適切な一連の手続きケースを開発する方法はありうる。
■プログラムの検査、ウォークスルー、検討
プログラミングの世界では多くの人々はプログラムとは単にコンピューターで実行するために書くものであって、人に読まれるように意図されておらず、コンピューターでそのプログラムを実行させる以外にプログラムテストの方法はない、という仮定のもとに働いていました。
今日、ソフトウェアアプリケーションの全てのテストする人はコードを読むわけではないがプログラムコードをテスト作業の一部として学ぶという概念は確かに広く受け入れられています。
与えられたテストとデバッグの作業は人々の実際にプログラムコードを読む事を含んでいることにはいくつかの要素が関係しています。
それはアプリケーションのサイズや複雑さ、開発チームの大きさ、アプリケーション開発の期間とプログラミングチームの背景と文化であります。
人間によるテスト技法はエラーを見つけるのに非常に効果的なので、これらの基本のいくつかをすべてのプログラム開発プロジェクトに取り入れたほうがいい、ということが明らかになりました。
ここで述べる手法はプログラムをコーディングするときとコンピューターによるテストを始めるときとの間に応用するためのものです。
人間によるテスト技法について述べる前にひとつ重要な注意をします。
人間の関与によってコンピューターによる数学的証明などより弱い形式的手法になっているからです。何かこのように簡単で非形式的なやり方は役に立たないのではないかという概念があります。
むしろこの技法は事実上、主として二つの点において生産性と信頼性に寄与をしています。
第一にエラーは早く発見すればするほどエラーの修正にかかるコストが低くなり同時にエラーを正しく修正する確率も高くなることが一般的に認められています。
第二にコンピューターによるテストが始まるとプログラマーは心理的に変化することであります。
内部で誘発された心的圧迫が急に増え、このつまらないバグをできるだけはやくなくしたいというように思うようになります。
この圧迫によって、プログラムは早期に発見されたエラーを修正する時もコンピューターによるテストの間に発見されるのを修正するときのほうが誤りが多くなります。
■検査とウォークスルー
コードの検査とウォークスルーの二つは人間によるテスト方法の基本的なものです。
この二つは非常に多くの共通点を持っています。検査とウォークスルーはチームの人々がプログラムを読む。または仮想的な検査が含まれている。この手法は両方とも参加者による準備過程を含んでいる。
本番は意見の会合つまり参加者によって開かれる会合である。この会合の目的はエラーを発見することでありエラーの解決法を見つけることではない。つまりデバッグをすることではなくテストすることである。
コードの検査とウォークスルーとはある期間広く使われてきたが、これらの手法の成功の理由はいくつかの原則と関連しています。
ウォークスルーは開発者グループによって検討されます。
3、 4人が適切である。そのうちの一人はプログラム作成者である。
プログラムテストの大部分は作成者よりも他の人々がテストするべきだろう。
これは普通、自分のプログラムをテストするには向いてないという原則に一致しています。また検査またウォークスルーとは、昔からある机上チェックの改良です。検査とウォークスルーははるかに効果的です。その理由はやはりプログラム作成者以外の人々による作業が含まれるからです。
ウォークスルーの利点はデバッグコストを抑えることにもなります。それはエラーを見つけるときエラーの正しい位置を知ることが多いからです。それに加えて、しばしばエラーをまとめて発見できるのでこれらのエラーを後でひとまとめにして修正できます。一方コンピューターのテストの場合は普通エラーの症状しか見つけられないのでエラーは通常一つずつ表示され修正されます。これらの手法では、典型的なプログラムの論理設計とコーディングエラーの30%から70%を見つけることに効果があります。しかしこの手法は要求分析の過程でのエラーのように高度な設計エラーには効果がありません。成功率が30%から70%とはすべてのエラーの70%までが見つけられるという意味ではないことに注意してほしい。
プログラムの中のエラーの合計は知ることができないからです。
■コードの検査
コードの検査とはグループによるコード読みをするための一連の手続きとエラー検出技法のことを言います。コード検査のほとんどの議論はそのコードの手続きと認められるべき表形式に集中しています。ここでは一般的な手続きの簡単な要約を述べた後、実際のエラー検出法に焦点を絞ります。
検査は普通4人で構成されます。4人のうち一人は議長の役目を果たし議長は有能なプログラムであるがそのプログラムを作成者ではない。
そのプログラムの詳細を知っている必要はない。
議長の責任は資料を準備して配布したり、検査会のスケジュールを立てその会を引っ張っていき
発見された全てのエラーを記録します。
そのエラーがその後修正されているかどうかを確かめることです。
議長は品質管理技術者に似た役割をします。
次にチームの一員として挙げられるのはプログラマーです。残りの構成は通常そのプログラムの設計者とテストの専門家であります。
1
プログラマーはプログラムの論理を一命令ずつ読み上げる。
その読み上げている間に他の参加者は疑問点を上げエラーがあるかどうかを判定することを求められる。発見されたエラーの多くは読み上げている最中に他の参加者によってよりも、そのプログラム作成者自身によって見つかることが非常に多いということです。
自分のプログラムを、声を出してみるというこの単純なことが著しい効果をあげているエラー検出法だと言えます。
2
これまでの経験から作られた共通のプログラミングエラーのリストを見ながらプログラムを分析する。
議長は議論が生産的な方向に進むように気を配り参加者がエラーを修正するのではなく見つけることに集中できるように考えなければならない。
検査後には発見されたエラーリストが残る。もし、かなりのエラーが見つかったり、あるいは相当な修正が必要とするエラーが見つかったら、エラーを修正した後のプログラムも再検査するように議長が調整します。
エラーリストを分析され分類され今後の検査をより効果的にするためのエラーチェックリストを充実させることができます。
検査に要する最適な時間は90分から120分くらいと思われます。
ほとんどの検査一時間当たり約150命令の速さで進められるので、大きなプログラムになると複数回の検査回によって調べる必要があります。
1回の検査では一つまた数個のモジュールあるいはサブルーチンを対象とします。
検索過程はまたエラーを見つけるという効果に加えていくつかの副次的効果をもたらします。
一つはエラーを見てこれらの誤りから学び取ることに加えて、そのプログラマーは自分のプログラミングスタイルやアルゴリズム選択プログラミング技術についてフィードバックを受けることができます。
他の参加者も、プログラムのエラーやプログラミングスタイルを調べることによって同様なことを得ることができます。
■検査のためのエラーチェックリスト
- データ参照エラー
- データ定義のエラー
- 計算エラー
- 比較エラー
- 制御流れのエラー
- インターフェースエラー
- 入出力エラー
- その他のチェック
■ウォークスルー
コードのウォークスルーとは検査と同様にグループによるコード読み合わせのための一連の手続きとエラー発見手法のことです。
検査と同様にウォークスルーは1、 2時間中断なしに行われる。
ウォークスルーのチームは3人から5人で構成されます。
一人は検査過程の議長とよく似た役割を演じます。
もう一人は書記の役割をします。
第三の人はテスト担当の役を果たします。
構成員の3から5人を誰にすべきかいろいろあります。
もちろんそのプログラムを作成したプログラマーも一員です。
ほかの参加者として次のような人々が挙げられます。
高度な経験を積んだプログラマー、プログラム言語の専門家、新人のプログラマー、そのプログラムを保守する予定の人、他のプロジェクトにいる人、プログラマーとして同じプログラミングチームにいる人。
最初の手続きは検査過程と同様です。
そのプログラムについて勉強する余裕のあるように数日前に資料を参加者に配布します。
しかし会合における手続きが異なります。
単にプログラムを読み上げたりエラーチェックリストを使ったりするのではなく、参加者はコンピューターを演じる。テスト担当者に示された人はテストケースをすこし書いた紙―そのプログラムまたモジュールに対する代表的な一連の入力データと予想できる出力データを用意して会合にやってきます。会合の間テストケースを頭の中で実行され、つまりテストデータでプログラムの論理にそって歩くのです。
プログラム状態つまり変数の値は紙の上また黒板上で監視されます。
もちろんテストケースは簡単な性質のもので少ない数でなければならない。
というのは人間は機械に比べてけた外れにゆっくりとした速度でプログラムを実行するからです。テストケースそのものは直接的な役割を演じないで、プログラムの論理や過程についてプログラムに質問を投げかけたりきっかけを掴んだりする媒介物の役目をします。
ほとんどのウォークスルーではテストケースそのものから直接エラーが見つけられることよりもプログラマーに質問する過程で多くのエラーが発見されています。
検査の時と同様に参加者の態度は重要です。意見はプログラマーではなくプログラムそのものに向けなければならない。
言い換えれば、それを出した人の弱点としてみないのであります。
エラーはプログラム開発の困難さに固有のものであり、これは現在のプログラミング手法がまだ原始的な状態である結果であると見なします。
■机上のチェック
つまり一人の人間で、プログラムを読みエラーリストまたはそれによるウォークスルーテストデータを見ながらチェックする。大抵の人にとっては机上チェックは比較的実りの少ないものです。
その理由の一つはこの過程が完全に規律のない過程であることが挙げられます。
第二により重要な理由は、テストの原則:―一般的に、人が自分のプログラムを作るのは効果がないという原則―に反することです。
■仲間内の評価
これはコードの読みやすさの考えに関係があります。仲間内の評価とは匿名のプログラムを全体の品質保守のしやすさ使いやすさ明晰さについて評価することです。
この手法の目的はプログラマーが自己評価ができるようにすることです。
一人のプログラムがこの過程の管理者として選ばれます。
管理者は次に6人から20人ぐらいの参加者を選出します。
参加者は同じような経験をもった同士が望ましい。
参加者はそれぞれ自分のプログラムのうち二つの検討に供するために選びます。そのうちのひとつはプログラムが自分の最高のできと思われるもの、もう一つは質が落ちると考えているものにします。プログラムが集まったら参加者に無作為に分配します。
参加者はそれぞれ四つのプログラムを検討するために与えられる。
二つのプログラムは最高のプログラムで、あとの二つは劣っているものであるが、検討者にはどれがどれであるか教えません。参加者はそれぞれのプログラムごとに30分を費やしそのプログラムを検討したのち評価表を完成します。
4つのプログラムをすべて検証検討したのち4つのプログラムを質の相対的比較を行ないます。
評価表上に、検討者は1から7までの尺度によって次のような質問に答えるように要求します。
このプログラムは理解しやすかったか
高いレベルでの設計は明確で適切か
低いレベルの設計は明確で適切か
このプログラムを変更するとすればそれは容易だと思われるか
このプログラムもあなたが書いたとしたらそれを誇りに思えるか
検討者は一般的な意見と助言できる改善策をも尋ねられます。
■テストケースの設計
可能なテストのどのようなサブセットがもっとも発見できる確率が高いか。
もっとも劣った手法はランダム入力テストです。
もっとも多くのエラーを発見できる確率という観点からはテストケースを無作為に選ぶのではなくテストケースを賢明に選択できる一連の思考過程である。
■ブラックボックス
- 同一分割
- 限界値分析
- 原因結果グラフ
- エラー推測
■ホワイトボックス
- 命令網羅
- 判定条件網羅
- 条件網羅
- 判定条件・条件網羅
- 複数条件網羅
■推奨する手続き
推奨する手続きとしてはブラックボックス法を使ったテストケースを開発しそしてホワイトボックス方を使って必要なだけ補足的なテストケースを開発することである。
■論理網羅テスト
ホワイトボックステストはそのテストケースがプログラムの論理を実行するかまたは網羅するようなものを考えられている。
有効な網羅基準はプログラムの全ての命令が少なくとも1回は実行されることである。
これは弱い条件である。
より強力な論理網羅の基準は判定条件網羅または分岐網羅として知られている。
■同値分割
1 適切なテストとしてあらかじめ定めてある目標に到達するために、開発すべきテストケースの数を二つ以上減少できること。
2 ほかの可能なテストケースのセットを広範囲にカバーしていること。
この二つの考えから同時分割と呼ばれるブラックボックス手法が作られる。
■同値クラスの見極め方
同一クラスを見分けるにはそれぞれの入力条件を取り上げ二つ以上のグループに分割することによって行う。
一つは有効同値クラス、
もう一つは無効同値クラスである。
■限界値分析
限界条件とは入力同値クラスと出力高値クラスの端の真上あるいはその上から下に位置する状況のことである。
限界値分析は次の点において同値分析とは異なる。
1 同値クラスの場合はその代表としてどんな要素を選んでも良いけれども限界値分析では同値クラスのそれぞれの端がテストの対象となるように、一つまたは複数個の要素を選ぶことが必要である。
2 入力条件または結果空間を考慮することによっても得られる。
限界値分析はかなりの想像力と問題に対するある程度の専門知識が必要であるからそのためのルールブックは難しい。しかしその一般的な指標を少し述べてみます
1入力条件が値の範囲を指定する場合その領域の両端のテストケースとそれらを超えた状態の無効入力テストケースを書く
2 入力条件がいくつかの値を指定する場合、値の数の最大値と最小数そして一つ少ない数と多い数のケースを書く
3 個々の出力条件について指標1を使う
4 個々の出力条件に指標2を適用する
5 プログラムの入出力データが1組の順序データセットである場合、その1組の最初の最初と終わりの要素に焦点を合わせる
6 加えて他の限界条件を見つけるための勘を働かせてほしい
■原因結果グラフ
原因結果グラフは自然言語で書かれた仕様が形式言語表現に翻訳されたものである。このグラフは実際はデジタル論理回路のようになるが標準的な電子工学的表現ではなく、もっと簡単な表現が使われる。プール論理の理解以外には電子工学的な知識が必要としない。
■エラー推測
人によっては生まれつきプログラムテストに精通していると言う思えるものがしばしば指摘されその一つの説明としてこのような人々は他の人よりももっと頻繁に無意識にエラー推測と呼ばれるようなテストケース設計行を実践している。ある特定のプログラムが与えられたとき、彼らは直感と経験からある種の起こりそうなエラーの形を推測して、これらのエラーを発見するためのテストケースを書くので、非常に直感的であり、場当たり的なやり方なので、エラー推測技法としての手順を示すことは難しい。
■戦略
テストケース設計方法は一つの連帯的戦略に統合できる。
これらを統合する理由は、それぞれの手法は有用なテストケースのうち、一部のセットには寄与するが、どれもそれだけではテストケースの全体のセットには寄与できない。
適切な戦略を次にあげると
1 仕様が入力条件の組み合わせを含んでいる場合は原因結果グラブの作成から始める
2 どんな場合でも限界値分析を行う
3 入力と出力の有効と無効の同値クラスを見分け、もし必要なら見分けたテストケースを補足する
4 さらに定数係数を得るためにエラー推測を使う
5 テストケースのセットを考慮に入れながらプログラムの論理を調べる。
判定条件網羅、条件網羅、判定条件・条件網羅、複数条件網羅の基準のうちのどれかを使う
■モジュールのテスト
モジュールテストは一つのプログラムの中のサブプログラム、サブルーチンのテスト過程を言う。
すなわちそのプログラムを最初から全体としてテストするのではなくまずプログラムのより小さな構成ブロックに焦点を当ててテストするのである。
これをする動機は三つある。
第一にモジュールテストは最初にプログラムの小さなユニットに着目するのであるからテストの組み合わせの要素を管理する。
第二にモジュールテストはエラーが見つかったときに特定のモジュールの中にあることがわかるので、デバッグ作業が容易になることである。
最後にモジュールテストは複数のモジュールを同時にテストする機会を与えてくれるのでテスト過程に並行処理を導入することができる。
モジュールテストの目的はあるモジュールの機能をそのモジュールを定義している機能仕様あるいはインターフェース仕様と比較することである。
全てのテストの目標を再び強調するために、ここでの目標はこのモジュールが仕様にあっていることを示すことではなく、モジュールが仕様に反していることを示すこと。
モジュールテストの過程は次の三つの観点から議論する。
1 テストケースを設計する方法
2 モジュールをテストして統合すべき順序
3 このテストを行う上での実際的助言
■テストケースの設計方法:増加テスト
モジュールテストを行う場合二つの鍵になる考察がある。
効果的な一連のテストケースの設計と、実際に稼働するプログラムを形成するためのモジュールを統合する方法とである。
二番目の考察は重要である。その理由は
モジュールテストケースを書く方法、用いるテスト道具の形、モジュールをコーディングしテストする順序、テストケースを作成するのにかかる費用、そしてデバッグの費用と関わり合いを持つからである。
各モジュールを別々にテストしてから、そのモジュールを統合してプログラムを形成するのか、または、テストすべき次のモジュールを、すでにテストしたモジュールのセットと結合してからテストするのか、ということである。
前者を非増加テストとよび、後者を増加テストと呼ぶ。増加テストは、非増加テストより優れているので、ここでは増加テストのみを説明する。
二つの増加テストの方法、それはトップダウンテストとボトムアップテストである。
トップダウンテスト、トップダウン開発、トップダウン設計、はしばしば同義語として使われているがトップダウンテストとトップダウン開発は同様であるが、トップダウン設計はかなり異なった全く独立したものである。
トップダウン設計したプログラムは、トップダウンかボトムアップのどちらの方法でも増加的にテストできる。
トップダウンテストはプログラムの頂上つまり最初のモジュールから始める。
その後増加的にテストすべき次のモジュールを選ぶための正しい手順はない。
唯一のルールは次のモジュールになる資格を得るためには少なくともそのモジュールを呼ぶモジュールのうちの一つは既にテスト済でなければならないということである。
ボトムアップテスト、ボトムアップ増加テスト方法を調べてみる。
ボトムアップテストはトップダウンテストと反対である。
トップダウンテストの長所はボトムアップテストの短所でありトップダウンテストの短所はボトムアップテストの長所になる。
ボトムアップはプログラム末端モジュールから始める。
末端のモジュールをテストしたのち増加的テストをするための次のモジュールを選択するための最良の手続きはやはり存在しない。唯一の規則は次のモジュールとして資格を持つにはそれはそれが呼ぶモジュールの全てがテスト済でなければならないということである。
■テストの実行
自動的なテスト道具を使うとテストの単調の苦しい仕事を最小にできる。
例えばドライバーモジュールの必要がなくなるようなテスト道具もある。
流れ分析道具と言ってプログラムを通り抜ける経路を列挙して決して実行されない命令を見つけ、値を割り当てないで変数を使ったりした場合を発見してくれるものもある。
モジュールテスト準備するとき心理学的、経済学的原則を検討すると役に立つ。
■上級テスト
ソフトウェアのエラーはプログラムを使うユーザーが当然のこととして期待していることを実行しない場合に現れる。
ソフトウエアの開発過程を図に示す。

開発過程とテスト過程の一致した場合の例を示す。
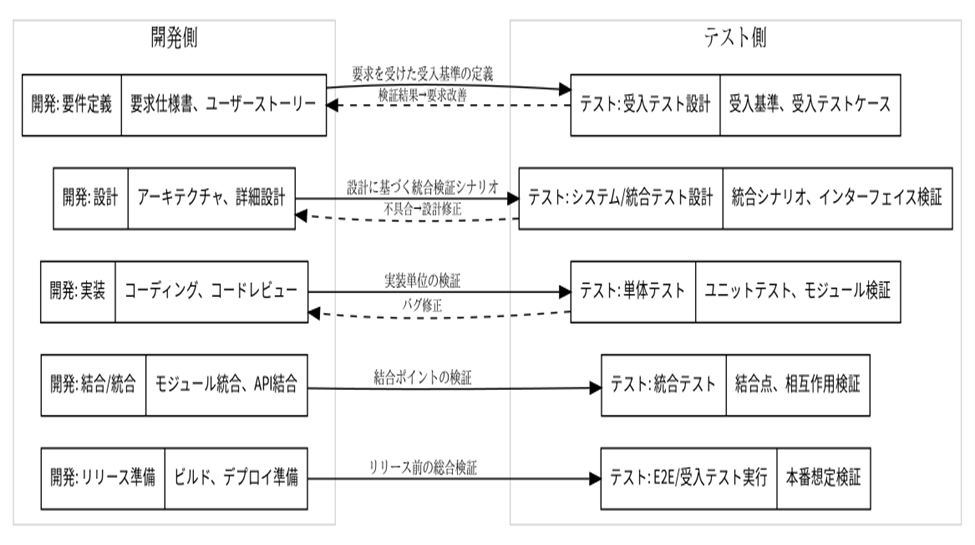
■デバッグ
デバッグはテストケースに成功したあとの仕事である。
(1)プログラム内で疑わしいエラーの正確な性質とあり場所を見つけること。
(2)エラーを修正すること。
プログラマーがもっともいやがる過程である。
■エラーの位置発見の原則
考えよ
行き詰った時は足に延ばそう
行き詰った時はその問題を他人に説明しよう
デバッグ道具は二番目の手段として使おう
実験を避けよう
実験は最後の手段である
■エラー修正の原則
一つのバグがある所には別のエラーもある可能性が高い
エラーの兆候ではなくエラーそのものを治そう
修正が正しいという確率は100%ではない
修正が新しい確率はプログラムが大きいほど落ちる
エラー修正は新しいエラーを生む可能性があることに注意しよう
エラー修正の時、しばらく設計段階に戻ってみよう
オブジェクトコードではなくソースコードを変更しよう
■エラー分析
プログラマーやプログラミング組織は発見されたエラーまた少なくともエラーの一部分を詳細に分析することによって成長できる。
これは困難で時間のかかる仕事である。
というのは分析をすることはエラーのXパーセントは論理設計のエラーであるとか、エラーの40%はif文の中で起きているといった、皮相的な分類よりもっと多くのことを意味しているからである。
注意深い分析としては次のような研究がある。
1 どこでエラーが起きたのか
2 誰がエラーを作ったのか
3 何が誤っておこなわれたのか
4 どうすればそのエラーを防ぐことができたのだろうか
5 なぜそのエラーは早期に発見されなかったのか
6 どうすればこのエラーはもっと早く発見できたのだろうか
発見された答えは、このあとのプログラミング処理を改善するのにはかりしれない価値を持ちうる。
■補足
最近のプロジェクト管理・プログラミング開発管理として、標準になりつつあるのは、アジャイルがありますが、その中心的なコンセプトは、XP(Extreme Programming)です。
以下は、アジャイルの開発過程を図にあらわしたものです。
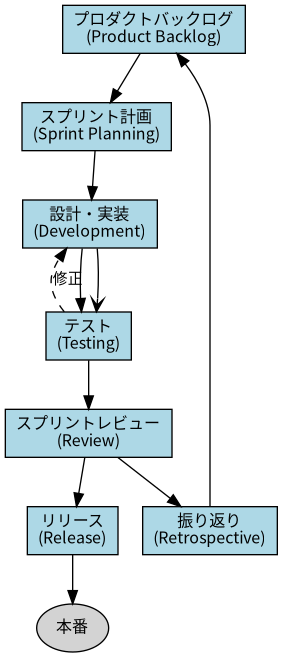
■参考
XP(Extreme Programming)
<Wikipediaより>
「エクストリーム・プログラミング、XPは、 ソフトウェア品質 を向上させ、変化する顧客の要求への対応力を高めることを目的としたソフトウェア開発プロセスである。アジャイルソフトウェア開発の一つとして、短い開発サイクルで頻繁に「リリース」することを推奨することで、生産性を向上させ、新しい顧客の要求を採用するためのチェックポイントを導入することを意図している。」
基本は、
1 顧客と他のプログラマに聞く。
2 アプリケーションの仕様とテストケース作成のために顧客と協働する。
3 プログラミング仲間といっしょにコード作成する。
4 そのコードでテストする。
■経験則
- イテレーションは1〜2週間を標準にする
- 小さなリリースを頻繁に行う
- 細かいデリバリでリスクを小さくし、学習サイクルを短縮する。
- テストファーストを徹底する
- 単体テスト→実装→リファクタリングのサイクルで設計が自然に良くなる。
- 継続的インテグレーション(CI)は必須
- 毎日(可能ならコミットごと)ビルド・テストを通す。
- ペアプログラミングで品質と共有を高める
- 設計の合意と知識伝播が進む。最初は短時間から試すと導入しやすい。
- コードの共同所有(Collective Ownership)
- だれでもどのコードでも修正できる。バグが出たら皆で直す文化。
- コーディング標準と簡単なレビュー習慣を明文化する。
- 常にリファクタリングを行う
- 新しい機能の追加時に設計を整える。技術的負債は早めに払う。
- 小さな安全なリファクタリングを繰り返す。
- 単純な設計(Keep It Simple)
- 今必要な機能だけを作る。複雑さは要求が出たときに追加。
- 設計判断は「現時点での最小限」で考えるチェックリストを持つ。
- オンサイトの顧客/プロダクトオーナーを確保する
- 優先度決定や仕様確認を即座に行えると無駄が減る。
- 代替として常に応答できるプロキシ担当を設ける。
- プランニングゲームで短期優先度を決める
- ビジネス価値と実装コストを併せて優先順位を決定する。
- ストーリーは小さくし、見積りと実績を比べて学習する。
- ペアと単独のバランスを取る
- ずっとペアでは疲れる。集中作業が必要な場合は単独時間を許可する。
- 重要タスクはペア、単純作業は個人で分担するルールを作る。
- 受け入れ基準と自動受け入れテストを明確にする
- ストーリー完了の定義をテストで担保する。
- 受け入れテストは顧客と一緒に作る。
- 持続可能なペース(週40時間)を守る
- 長時間労働は短期の生産性は出ても長期で崩れる。
- 突発対応は緊急ルールを設け、常態化させない。
- 技術的負債は可視化して計画的に返す
- ダッシュボードやカード化して管理する。
- ペアレビューよりも「動くソフト」とテストを信頼する
- コードレビューは重要だが、動いてテストが通ることが最大の証拠。
- プロトタイプ(スパイク)は短時間で見切る
- 技術不明点は短時間で検証し成果は廃棄前提で扱う。
- 見積りは相対見積りで改善する
- 初期は粗い見積りで良い。過去の実績から精度を上げる。
- 指定された言語(ユビキタス言語)を使う
■参考2
図のようにそれぞれの接点すなわち丸印は逐次的に実行される命令文を表し分岐命令で停止可能です。
それぞれの矢印は命令群間の制御の流れをあらわし、この図は最高20回繰り返すDOループを持つ10から20ステップのプログラムを表しています。
ルールの中には一連のテストされたif命令があります。
異なった論理経路の数を決定することはa点からb点に行くことになる道順の数を見つけるのと同じです
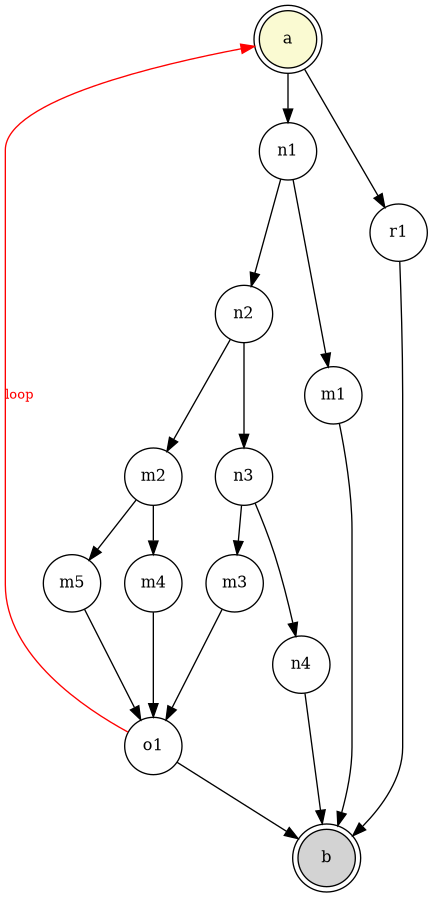
下記のプログラムの実行結果:
Single-iteration counts:
backedge_sources = ['o1']
R = 3
E' = 6
DP (unrolled) total paths (0..20 loops): 31381059606
Closed-form total: 31381059606
Match DP vs closed-form: True
■プログラム
#!/usr/bin/env python3
# Count paths for the provided graph with backedge o1->a, max iterations N=20
from collections import defaultdict, deque
graph = {
'a': ['n1', 'r1'],
'n1': ['n2', 'm1'],
'n2': ['n3', 'm2'],
'n3': ['n4', 'm3'],
'n4': ['b'],
'm1': ['b'],
'm2': ['m5', 'm4'],
'm3': ['o1'],
'm4': ['o1'],
'm5': ['o1'],
'o1': ['b', 'a'], # backedge to a
'r1': ['b'],
'b': []
}
loop_nodes = {'a','n1','n2','n3','m1','m2','m3','m4','m5','o1'}
header = 'a'
N = 20
def build_unrolled_graph(graph, loop_nodes, header, N):
G = defaultdict(list)
def name(node, k): return f"{node}_{k}"
nodes = set(graph.keys()) | {v for vs in graph.values() for v in vs}
for u in nodes:
for v in graph.get(u, []):
if u not in loop_nodes and v not in loop_nodes:
G[name(u,0)].append(name(v,0))
elif u not in loop_nodes and v in loop_nodes:
G[name(u,0)].append(name(v,0))
elif u in loop_nodes and v not in loop_nodes:
for k in range(0, N+1):
G[name(u,k)].append(name(v,0))
else:
if v == header:
for k in range(0, N):
G[name(u,k)].append(name(v,k+1))
else:
for k in range(0, N+1):
G[name(u,k)].append(name(v,k))
all_nodes = set(G.keys()) | {v for vs in G.values() for v in vs}
for n in all_nodes:
G.setdefault(n, [])
return G
def count_paths_dag(G, start_node, end_node):
indeg = defaultdict(int)
nodes = set(G.keys()) | {v for vs in G.values() for v in vs}
for u in G:
for v in G[u]:
indeg[v] += 1
indeg.setdefault(u, 0)
q = deque([n for n in nodes if indeg[n] == 0])
topo = []
while q:
u = q.popleft()
topo.append(u)
for v in G.get(u, []):
indeg[v] -= 1
if indeg[v] == 0:
q.append(v)
paths = defaultdict(int)
paths[start_node] = 1
for u in topo:
if paths[u] == 0: continue
for v in G.get(u, []):
paths[v] += paths[u]
return paths[end_node], paths
def compute_single_iteration_counts(graph, loop_nodes, header, end_node):
# build single-iteration graph by removing edges u->header (backedges)
G1 = defaultdict(list)
nodes = set(graph.keys()) | {v for vs in graph.values() for v in vs}
backedge_sources = [u for u in nodes if (u in loop_nodes) and (header in graph.get(u, []))]
for u in nodes:
for v in graph.get(u, []):
if u in loop_nodes and v == header:
continue
G1[u].append(v)
# topological DP (G1 is acyclic after removing backedges)
indeg = defaultdict(int)
all_nodes = set(G1.keys()) | {v for vs in G1.values() for v in vs}
for u in G1:
for v in G1[u]:
indeg[v] += 1
indeg.setdefault(u, 0)
q = deque([n for n in all_nodes if indeg[n] == 0])
topo = []
while q:
u = q.popleft()
topo.append(u)
for v in G1.get(u, []):
indeg[v] -= 1
if indeg[v] == 0:
q.append(v)
paths = defaultdict(int)
paths[header] = 1
for u in topo:
for v in G1.get(u, []):
paths[v] += paths[u]
E_prime = paths[end_node]
R = sum(paths[s] for s in backedge_sources)
return R, E_prime, backedge_sources
def main():
R, E_prime, backedge_sources = compute_single_iteration_counts(graph, loop_nodes, header, 'b')
print("Single-iteration counts:")
print(" backedge_sources =", backedge_sources)
print(f" R = {R}")
print(f" E' = {E_prime}")
# DP on unrolled graph
G_unrolled = build_unrolled_graph(graph, loop_nodes, header, N)
start_node = f"{header}_0"
end_node = "b_0"
total_dp, _ = count_paths_dag(G_unrolled, start_node, end_node)
print(f"\nDP (unrolled) total paths (0..{N} loops): {total_dp}")
# closed-form
if R == 1:
total_formula = E_prime * (N+1)
else:
total_formula = E_prime * (pow(R, N+1) - 1) // (R - 1)
print(f"Closed-form total: {total_formula}")
print("Match DP vs closed-form:", total_dp == total_formula)
if __name__ == '__main__':
main()
著者:松尾正信
株式会社京都テキストラボ代表取締役
